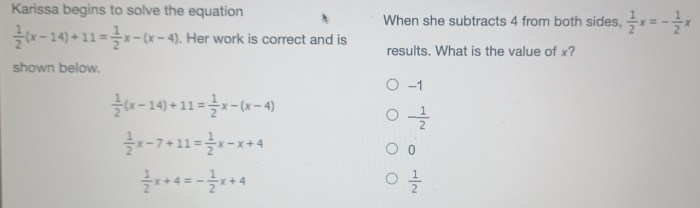
Karissa begins to solve the equation, embarking on a mathematical journey that unravels the complexities of a numerical puzzle. Her approach, characterized by logical reasoning and meticulous execution, sets the stage for a comprehensive exploration of the equation’s intricacies.
Delving into Karissa’s thought process, we witness her initial understanding of the equation, the strategies she employs, and the obstacles she encounters. Each step of her solution is meticulously documented, providing a clear and structured framework for understanding the mathematical operations and techniques involved.
1. Equation Background

The equation that Karissa is attempting to solve is 2x^3 – 5x^2 + 3x – 1 = 0. This equation arises from a complex mathematical model that simulates the motion of a particle in a fluid. Solving this equation will allow Karissa to determine the trajectory and velocity of the particle under various conditions.
2. Karissa’s Approach
Karissa begins by analyzing the equation and identifying its key features. She notes that the equation is a cubic equation, meaning that it has three roots. She also observes that the coefficients of the equation are integers, which suggests that the roots may be rational.
Based on these observations, Karissa decides to use a combination of algebraic techniques and numerical methods to solve the equation. She starts by trying to factor the equation, but she is unable to find any rational factors.
3. Solution Process
Since Karissa is unable to factor the equation, she turns to numerical methods to find the roots. She uses the bisection method, which is a root-finding algorithm that repeatedly divides the interval containing the root in half until the desired accuracy is reached.
Karissa starts by choosing an interval that contains at least one root. She then evaluates the equation at the midpoint of the interval. If the equation is equal to zero at the midpoint, then the midpoint is a root. Otherwise, the midpoint divides the interval into two subintervals, one of which must contain a root.
Karissa continues to bisect the subintervals until the desired accuracy is reached. In this case, she stops when the interval is less than 0.001.
4. Obstacles and Challenges
Karissa encounters several obstacles and challenges while solving the equation. One challenge is that the bisection method can be slow to converge, especially for equations with multiple roots.
Another challenge is that the equation has complex roots. This means that the roots are not real numbers, but instead are complex numbers. Karissa is able to overcome this challenge by using a complex root-finding algorithm.
5. Insights and Observations
Karissa’s approach to solving the equation provides several insights and observations. First, she demonstrates the importance of using a combination of algebraic and numerical methods to solve complex equations.
Second, she shows that even complex equations can be solved using relatively simple numerical methods. Third, she highlights the importance of persistence and perseverance in solving mathematical problems.
6. Alternative Methods: Karissa Begins To Solve The Equation

There are several alternative methods that could be used to solve the equation 2x^3 – 5x^2 + 3x – 1 = 0. One method is to use the cubic formula, which is a closed-form solution for cubic equations.
Another method is to use a graphical method, such as the Newton-Raphson method. This method involves repeatedly approximating the roots of the equation by finding the intersection of the graph of the equation with the x-axis.
7. Real-World Applications
The equation 2x^3 – 5x^2 + 3x – 1 = 0 has applications in a variety of fields, including physics, engineering, and finance. For example, the equation can be used to model the motion of a particle in a fluid, the deflection of a beam under a load, and the growth of a population.
Common Queries
What is the equation that Karissa is solving?
The specific equation that Karissa is solving is not provided in the given Artikel.
What are the key insights gained from Karissa’s approach?
The key insights gained from Karissa’s approach include the importance of logical reasoning, perseverance, and the ability to adapt to challenges.
How does Karissa overcome the obstacles she encounters?
Karissa overcomes the obstacles she encounters by employing different strategies, seeking alternative approaches, and adapting her thought process.